Fraktale – Inspiration für Procedural Generation

Fraktale sind faszinierende Strukturen, um sowohl Artists als auch Programmierer zu inspirieren, sich mit Procedural Generation auseinanderzusetzen, das in Computerspielen und Filmen dazu beitragen kann, mit vertretbarem Aufwand grosse und detaillierte digitale Welten zu erzeugen.

Fraktale sind faszinierende Strukturen, um sowohl Artists als auch Programmierer zu inspirieren, sich mit Procedural Generation auseinanderzusetzen, das in Computerspielen und Filmen dazu beitragen kann, mit vertretbarem Aufwand große und detaillierte digitale Welten zu erzeugen. Abwechslungsreiche, detaillierte und weiträumige digitale Welten tragen zu einem lebendigeren und interessanteren Eindruck in Computerspielen und Filmen bei. Procedural Generation kann eingesetzt werden, um den Aufwand dafür stark zu reduzieren, erfordert aber die Grenze zwischen Programmierer und Artist durchlässiger zu machen. Da Fraktale in der Procedural Generation eine wichtige Rolle spielen, vom künstlerischen Standpunkt aus interessant sind und teils bereits mit minimalistischen Programmen erzeugt werden können, eignen sie sich sowohl für Programmierer als auch für Artists als Einstieg in das Thema. Procedural Generation bedeutet, dass Content durch Algorithmen erzeugt bzw. »berechnet« statt mper Hand modelliert und platziert wird. Anstatt unmittelbar ein Objekt nach dem anderen zu entwerfen, hat der Designer Einfluss auf Regeln, die bestimmen, wie neue Objekte automatisch (mit zufälligen Variationen) generiert und wo sie positioniert werden. Betrachten wir im Folgenden einige Anwendungsbeispiele. Eine Auswahl von Software zur Procedural Generation: • Terragen [1] • City-Engine [2] • Speed-Tree [3] Eine Auswahl von Spielen die Procedural Generation einsetzen (u. a. nach [4]): • Minecraft (2011) • Spore (2008) • Hellgate: London (2007) • Diablo 2 (2000) • Worms (1995) • Elite (1984) • Nethack (1987) • Rogue (1980) Ein prominentes Beispiel für Procedural Generation in Filmen: Die Wälder des Planeten Pandora im Spielfilm Avatar wurden mit SpeedTree erstellt. [5] Procedural Generation verspricht viele Vorteile: endlose, abwechslungsreiche, detaillierte Welten, erzeugt in kurzer Zeit und mit relativ wenig Aufwand. Dies gilt allerdings nur, wenn die entsprechende Software vorhanden und einsatzreif ist. Für unterschiedliche »hand-gearbeitete« 3d-Modelle (Gebäude, Vegetation, Terrain...) kann immer das gleiche Modellierungs-Programm verwendet werden. Procedural Generation dagegen erfordert oft an die Aufgabe angepasste Software: Häuser? City-Engine! Bäume? Speed-Tree! Berge? Terragen! Ein »Prozedurales-Tool-für-alles« würde dieses Problem auch nicht lösen, denn je allgemeiner ein Programm ist, desto mehr Konfiguration erfordert es, bis diese schließlich darauf hinausläuft, eben die speziellen Generierungs-Programme zu schreiben – nur eben in einer Skript-Sprache statt z. B. in C++. Es sieht so aus, dass Projekte, in denen Procedural Generation zum Einsatz kommt, zwar weniger Artists erfordern, dafür aber umso mehr Programmierer. Genauer gesagt lässt Procedural Generation die Trennung zwischen Programmierern und Artists verschwimmen: Es reicht nicht, »nur« komplexe, effiziente Programme schreiben zu können oder »nur« geniale, kreative Werke zu schaffen – beides muss kombiniert werden: Procedural Generation erfordert Programmierer-Artists bzw. Artist-Programmierer, die wissen, durch welchen Algorithmus, welche mathematische Formel sich eine gewünschte Struktur (Gebäude, Pflanzen, Gebirge...) erzeugen lässt, und brauchen Kreativität, Farbgefühl, einen Sinn für Proportionen etc. damit die Qualität des Ergebnisses dem »per Hand« modellierten Äquivalent entspricht. An dieser Stelle lohnt sich ein Blick auf die Demo-Szene. Hier finden Wettbewerbe statt, in denen es darum geht mit einem möglichst kleinen (z. B. nur 64KB oder sogar nur 4 KB) Programm einen möglichst beeindruckenden Effekt zu erzeugen, wie etwa (Elevated [6]), eine fotorealistische Kamera-Fahrt über ein Gebirge oder (KKrieger [7]), einem »Shooter« in 96 KB. Die Selbstbeschränkung auf derart kleine Programme, bei gleichzeitig hohem künstlerischen Anspruch, ist nur mit massivem Einsatz von Procedural Generation möglich. Ein die Symbiose von Programmierung und Design ansprechendes Zitat aus der Demo-Szene (in ähnlicher Form immer wieder im Web zu lesen) lautet frei übersetzt: »Unser Design-Werkzeug ist der C++ Compiler«. Eine wichtige Rolle für Procedural Generation spielen Fraktale bzw. L-Systeme neben Perlin-Noise. Gebirge können u. a. per Midpoint-Displacement, (animierte) Wolken durch Überlagerung von Perlin-Noise [8], [9] unterschiedlicher Frequenzen und Pflanzen oder auch Städte mittels L-Systemen erzeugt werden. Wie lässt sich von Anfang an Interesse an dieser Schnittstelle zwischen Programmierung und Design bei Game-Design Studenten wecken? Obwohl Procedural Generation beliebig komplex werden kann, lassen sich schon mit sehr kleinen, kompakten Programmen beeindruckende Ergebnisse erreichen – genau dies ist gefragt, um Studenten zu motivieren, sich mit diesem Gebiet näher zu beschäftigen. Ein Kandidat für solche »Motivations-Programme« sind Fraktale: selbstähnliche mathematische Strukturen, die aus wiederholter Anwendung (Iteration) einer einfachen Rechenvorschrift entstehen und dabei unerwartet abwechslungsreiche, auch ästhetisch faszinierende Bilder ergeben. Im folgenden Abschnitt wird so ein minimalistisches Programm vorgestellt.

Ein Fraktal in C++: die Mandelbrot-Menge

Erklärungen zum Programmablauf

1. Eine Library einbinden, die Befehle zur Verfügung stellt, mit denen u. a. in eine Datei geschrieben werden kann.
2. Der Programm-Ablauf beginnt hier, in der main-Prozedur (die Standard-Parameter werden ignoriert).
3. Variablen initialisieren: Pixel-Breite und -Höhe (w, h) des zu erstellenden Bildes, Anzahl der Berechnungs-Iterationen N, Spaltennummer und Zeilennummer der Pixel-Position (u, v), aktuelle Iteration n, Koordinaten des dem Pixel entsprechenden Punktes in der komplexen Zahlenebene (x, y), zu iterierender Punkt (z_x, z_y), Konstante (c_x, c_y) sowie temporäre Variablen (nx, ny).
4. .pgm-Datei öffnen. Header des Portable Gray Map Formats10 schreiben. Das resultierende Bild kann mit einem Viewer wie z. B. IrfanView oder einem Bild-Editor wie z. B. GIMP betrachtet werden.
5. Schleife über alle Zeilen des Bildes
6. Schleife über alle Spalten des Bildes
7. Komponenten der Pixel-Position in Wertebereich [-1, +1] umrechnen (Normalized Device Coordinates).
8. Startwert und Konstante setzen sowie Bildausschnitt festlegen: für die Mandelbrot-Menge c = (x, y), z = 0, für die Julia-Menge z.B. c = (-0.95, 0.25), z = (x, y).
9. Iterationsschleife bis die Abbruch-Bedingung erfüllt ist, also entweder n die maximale Anzahl Iterationen N überschreitet oder der Punkt z den Abstand 2 zum Ursprung überschreitet (Achtung: Im Programm sind hier aus Effizienz-Gründen beide Seiten der Gleichung quadriert!) ...
10. ...wird die Berechnung (in komplexen Zahlen: z_neu = z_alt^2 + c wiederholt.
11. Ausgabe der Iterations-Anzahl als Pixel-Grauwert (im Intervall [0, 255]).
12. Zeilenumbruch nach jeder Bild-Zeile ausgeben (optional).
13. Um dieses Programm zum laufen zu bringen ist ein C++ Compiler notwendig. Unter Windows ist z. B. Visual-Studio (Express)11 kostenlos erhältlich.

Unter Linux ist der Gnu C Compiler12 standardmäßig mit dabei. Aufruf: g++ fractal.cpp -o fractal ./ fractal

Ausblick 3d-Fraktale rendern

Gute Visualisierung von 3d-Fraktalen ist um einiges schwieriger als im 2d-Fall. Oft kommen Ray-Tracing Verfahren zum Einsatz, so etwa bei Mandelbulber [13]. Einige Viewer, wie z. B. Boxplorer [14] nutzen Distance Estimation (gut erklärt in [15]) um das Ray-Tracing auf Echtzeit zu beschleunigen. Es wäre interessant, so eine fraktale Welt in ein Computerspiel einzubauen (gemeint ist hier eine über das übliche Midpoint-Displacement/Perlin-Noise Gebirge hinausgehende, eher mit einer Mandelbulb oder Mandelbox vergleichbare Welt). Herausforderung an Designer und Programmierer wäre dabei, die Fraktale soweit zu zähmen, dass sie sich als Spiel-Welt eignen, aber nicht soweit, dass sie ihre interessanten Eigenschaften (Selbstähnlichkeit, Komplexität, Größe, Details...) verlieren.

Anhang: die Formeln

Mandelbrot (2d) Iterationsformel, die Benoit B. Mandelbrot untersuchte:   (entdeckt von Pierre Fatou und Gaston Julia) bzw. aufgeteilt auf reele Komponenten 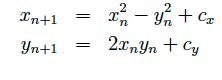Mandelbulb (3d) Versuch einer Erweiterung auf drei Dimensionen von Daniel White[20]: aus dem Winkel der Dreh-Streckung in der komplexen Zahlenebene werden Polarkoordinaten, der Exponent erhöht sich von 2 auf 8. 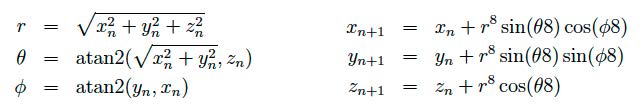Mandelbox (nd) Keine direkte Erweiterung der Mandelbrot-Menge auf höhere Dimensionen sondern von Entdecker Tom Lowe [21] zu Ehren Benoit Mandelbrots so benannt. Die Iterations-Formel der Mandelbox ist so beschaffen, dass sie mit einer beliebigen Anzahl an Dimensionen berechenbar ist. Sei ein beliebig dimensionaler Vektor, mit sowie wobei für a jede Achse des Koordinatensystems einmal eingesetzt wird. [1] Planetside: Terragen http://www.planetside.co.uk/ [2] Procedural: City-Engine http://www.procedural.com/cityengine/ [3] Interactive Data Visualization, Inc.: Speed-Tree http://www.speedtree.com/ [4] Wikipedia: Procedural Generation, http://en.wikipedia.org/wiki/Procedural_generation [5] Interactive Data Visualization, Inc.: SpeedTree In Avatar http://www.speedtree.com/avatar/ [6] Inigo Quilez: finalized works, http://www.iquilezles.org/prods/index.htm [7] The Produkkt: KKrieger, http://www.theprodukkt.com/kkrieger [8] David S. Ebert, F. Kenton Musgrave, Darwyn Peachey, Ken Perlin, Steve Worley: Texturing & Modeling { A Procedural Approach (Third Edition) The Morgan Kaufmann Series in Computer Graphics [9] Ken Perlin http://mrl.nyu.edu/~perlin/ [10] Wikipedia: Netpbm format (Portable Gray Map), http://en.wikipedia.org/wiki/Portable_Gray_Map [11] Microsoft: Visual Studio (Express), http://www.microsoft.com/visualstudio/en-us/products/2010-editions/visu… [12] GNU: GNU Compiler Collection, http://gcc.gnu.org/ [13] Krzysztof Marczak: Mandelbulber, http://sites.google.com/site/mandelbulber/ http://sourceforge.net/projects/mandelbulber/ [14] Jan Kadlec (aka Rrrola): Boxplorer, http://rrrola.wz.cz/downloads.html#effects http://sourceforge.net/projects/boxplorer/ [15] Mikael Hvidtfeldt Christensen: Distance-Estimation, http://blog.hvidtfeldts.net/index.php/category/distance-estimation/ [16] Daniel White: The Unravelling of the Real 3d Mandelbulb, http://www.skytopia.com/project/fractal/mandelbulb.html [17] Krzysztof Marczak: Mandelbulber, http://sites.google.com/site/mandelbulber/http://sourceforge.net/projec… [18] Tom Lowe (aka tglad): Mandelbox, http://sites.google.com/site/mandelbox/ [19] Jan Kadlec (aka Rrrola): Boxplorer, http://rrrola.wz.cz/downloads.html#effects http://sourceforge.net/projects/boxplorer/ [20] Daniel White: The Unravelling of the Real 3d Mandelbulb, http://www.skytopia.com/project/fractal/mandelbulb.html [21] Tom Lowe (aka tglad): Mandelbox, http://sites.google.com/site/mandelbox/

#im fokus #game design