Grafik-Programmierung für's Game-Development

Grafik-Karten Programme (Shader genannt) sind mittlerweile in Computerspielen allgegenwärtig. Sie sind meist relativ klein, schnell, auf eine konkrete Aufgabe zugeschnitten, robust und Engine-unabhängig. Kurz gesagt: ein schönes Übungs-Feld, in dem sich angehende Computer-Spiele Programmierer austoben können. Mit überschaubarem Aufwand lassen sich mit Shadern beeindruckende Ergebnisse erzielen und dabei die mathematischen Fertigkeiten üben.

Normale Programme (wie z.B. Web-Browser, Text-Verarbeitung u.ä.) werden auf dem Haupt-Prozessor des Computers (Central Processing Unit, kurz: CPU) ausgeführt, können sehr groß und komplex sein und haben zumindest im Prinzip Zugriff auf die gesamten Ressourcen des Rechners (Festplatte, Bildschirm, Lautsprecher, Netzwerk...). Grafikkartenprogramme, Shader genannt, sind dagegen kleiner und einfacher, haben wenig Speicher zur Verfügung und nur sehr eingeschränkte Kommunikationsmöglichkeit mit der Auflenwelt (sie liefern als Ergebnis ihrer Berechnung im Prinzip nur eine Handvoll Zahlen). Dafür werden sehr viele Instanzen eines Shader-Programms gleichzeitig ausgeführt.

Es gibt einige unterschiedliche Sorten von Grafik-Programmen in der Rendering- bzw. Grafik-Pipeline: Vertex-, Geometry-, Tessellation- sowie Pixel- bzw. Fragment-Shader.

Wir befassen uns hier nur mit Pixel-Shadern (auch Fragment-Shader genannt). Vereinfacht gesagt wird so ein Programm für jeden Pixel des Bildes gleichzeitig aufgerufen, wobei es als Eingabe die Koordinaten des Pixels als 2d-Vektor erhält und die Farbe des Pixels als 4d-Vektor (Rot, Grün, Blau, Opazität) ausgibt.

Erfahrungsgemäß macht Praxis-Bezug Programmierung interessanter. Glücklicherweise liegt die Einstiegs-Hürde bei der Grafik-Programmierung relativ niedrig: Es gibt einige Web-Seiten auf denen (dank Web-Gl) Shader interaktiv entwickelt und auf Knopfdruck (bzw. Maus-Klick) ausgeführt werden können. Die Beispiele in diesem Artikel sind kompatibel zu ShaderToy gehalten (https://www.shadertoy.com/new). Betrachten wir zunächst einen einfachen Shader, der die Koordinaten jedes Pixels als Farbe ausgibt, und so einen Farbverlauf erzeugt:

void mainImage(out vec4 c, vec2 p)
{
p /= iResolution.xy;
c = vec4(p,0,1);
}

Hierbei ist der zwei-dimensionale Vektor p die Pixel-Position, dessen horizontale Komponente p.x Werte von 0 bis zur Breite des Fensters annimmt und dessen vertikale Komponente p.y Werte von 0 bis zur Höhe des Fensters annimmt. Als erstes wird die Position Komponentenweise durch die Auflösung dividiert, um zu erreichen, dass die Komponenten nun Werte im Intervall von 0 bis 1 annehmen. Schliefllich wird als Ergebnis ein vier-dimensionaler Farb-Vektor c erzeugt, der als Rot-Anteil die horizontale Komponente der Position und als Grün-Anteil die vertikale Komponente der Position erhält. Der Blau-Anteil wird ausgeschaltet (auf 0 gesetzt) und die Opazität (Gegenteil von Transparenz) auf 1, also 100%. Im Gegensatz zur subtraktiven Farbmischung mit den Grundfarben Cyan, Magenta und Gelb wie sie beim Farb-Druck zu finden ist, arbeitet der Computer mit additiver Farbmischung, mit den Licht-Grundfarben Rot, Grün, Blau, d.h. vereinfacht gesagt mit den drei Farbtönen die den Rezeptoren im menschlichen Auge entsprechen. Das Ergebnis ist ein Farbverlauf (um die Anzeige zu aktualisieren muss man in ShaderToy den "Play"-Knopf anklicken).

Da Ausgabemöglichkeiten eines Pixel-Shaders so eingeschränkt sind, bietet es sich an, Zahlen als Farben darzustellen. Mit etwas Übung lassen sich die Farben dann als drei-dimensionale Vektoren "lesen": schwarz entspricht (0,0,0), weiß (1,1,1), blau (0,0,1), gelb (1,1,0) usw. Die resultierenden Werde werden übrigens in das Intervall [0,1] geclamped, d.h. alle negativen Komponenten werden als 0 und alle Komponenten gröfler als 100% als 1 interpretiert.

Versetzen wir uns nun gedanklich in folgende Situation: Für das User-Interface eines Computerspiels soll ein Timer implementiert werden, der den Fortschritt einer Aktion visualisiert bzw. die Wartezeit bis eine bestimmte Spiel-Funktion freigeschaltet wird.

Als erstes wählen wir eine einfache Visualisierung: einen von links nach rechts zunehmenden Balken, auf schwarz-transparentem Hintergrund. Der Einfachheit halber behalten wir den Farbverlauf bei.

void mainImage(out vec4 c, vec2 p)
{
p /= iResolution.xy;
c = vec4(0);
if(p.y > 0.4 && p.y < 0.6 &&
p.x < fract(iDate.w))
c = vec4(p,0,1);
}

Zwischen der ersten und der letzten Zeile sind Anweisungen hinzugekommen:

c = vec4(0);

sorgt dafür, dass ein Pixel im Zweifelsfall schwarz und transparent ist (Rot, Grün, Blau und Opazität werden mit dem Wert 0 initialisiert).

Die if-Anweisung prüft für jeden Pixel, ob dessen vertikale Positions-Komponente innerhalb des Intervalls [0.4,0.6] liegt

p.y > 0.4 && p.y < 0.6

UND die horizontale Positions-Komponente kleiner als ein bestimmter Wert ist. Dieser Wert müsste in der Praxis an die Spiele-Logik gekoppelt sein. Um die Funktion unabhängig davon testen zu können verwenden wir hier die Zeit in Sekunden (in Shadertoy die globale Variable iDate.w), genauer gesagt nur die Nachkommastellen (mittels fract) davon, so dass sich die Animation jede Sekunde wiederholt.

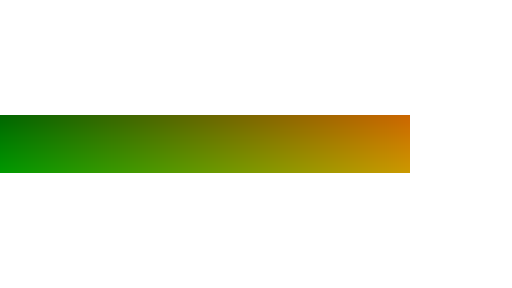
Um es etwas interessanter zu machen entscheidet jetzt die Design-Abteilung unserer fiktiven Spiele-Firma, dass eine lineare Visualisierung langweilig aussieht und stattdessen eine kreisförmige erwünscht ist. Um das zu erreichen müssen wir das Koordinatensystem wechseln.

Bisher verwenden wir ein orthogonales (kartesisches) Koordinatensystem.

Um den Ursprung in die Mitte des Bildes zu verschieben, ersetzen wir die erste Zeile durch

p = 2.0*p/iResolution.xy-1.0;

Die linke untere Ecke ist auf die Koordinate (-1,-1) abgebildet, die rechte obere Ecke auf (+1,+1). Diese Einstellung wird als Normalized Device Coordinates bezeichnet.

Nach dieser Zeile bietet es sich an das Seitenverhältnis zu korrigieren

p.x *= iResolution.x/iResolution.y;

Interessant wird es, wenn wir zu polaren Koordinaten wechseln. Diese bestehen aus dem Winkel um den, und Abstand zum, Ursprung. Den Abstand können wir durch length(p) ermitteln, den Winkel mit der Funktion atan(p.y,p.x). An dieser Stelle treten ein paar lästige Detail-Probleme auf: atan liefert Werte im Intervall [-pi,+pi] während für uns das Intervall [0,1] praktischer wäre. Um die Abbildung vorzunehmen teilen wir durch 6.28, was näherungsweise 2 pi entspricht, und nutzen die fract Funktion, um die Werte von [-0.5,+0.5] auf [0,1] abzubilden.

p = vec2(fract(atan(p.y,p.x)/6.28),
length(p));

Das fertige Pixel-Shader-Programm:

void mainImage(out vec4 c, vec2 p)
{
p = 2.0*p/iResolution.xy-1.0;
p.x *= iResolution.x/iResolution.y;
p = vec2(fract(atan(p.y,p.x)/6.28),
length(p));
c = vec4(0);
if(p.y > .4 && p.y < .6 &&
p.x < fract(iDate.w))
c = vec4(p,0,1);
}

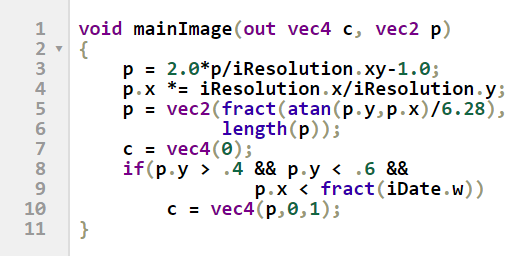
visualisiert einen Kreisförmigen Timer,

abgebildet bei einem Stand von 80%.

Dieser Timer könnte nun z.B. als Fortschrittsanzeige über ein Icon im User-Interface eines Spiels gelegt werden.

#im fokus #dozenten #game design #münchen